强化学习入门

RL笔记——《强化学习的数学原理 》

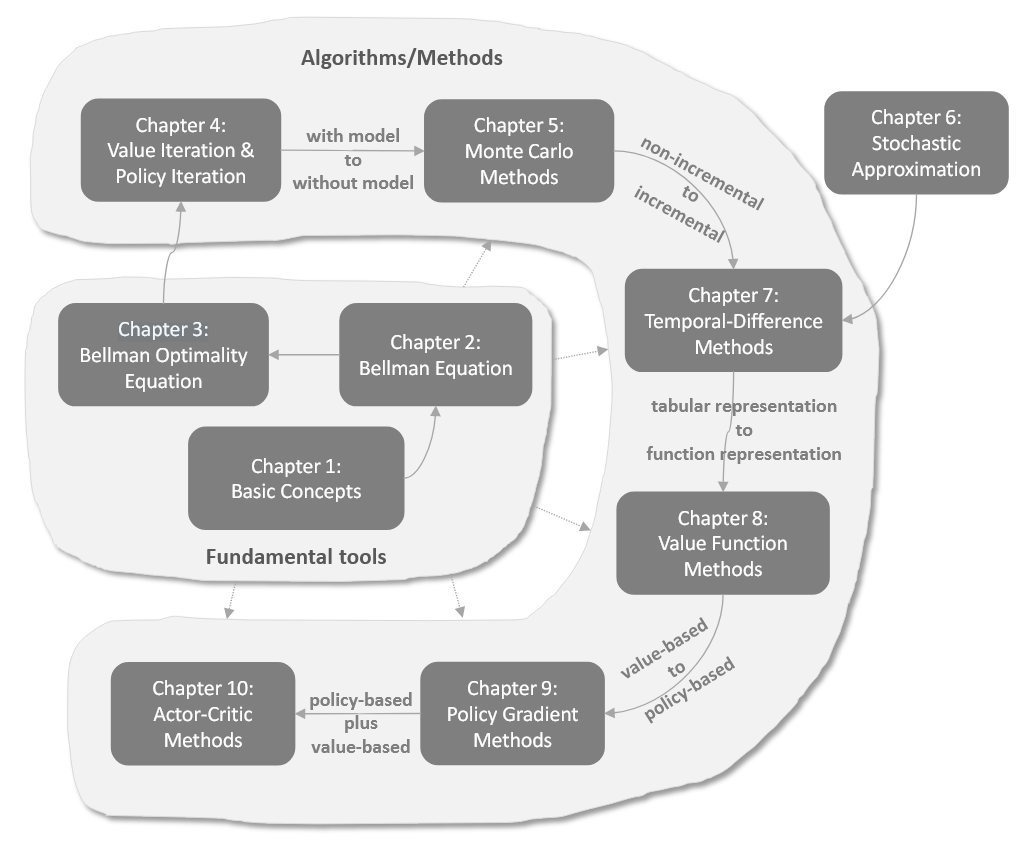
Roadmap镇楼。

1. 基本概念

State，Action

State transition

Reward

Trajectory，returns，episodes

MDP

2. 状态和Bellman方程

$v_\pi(s)$：State value，从一个状态出发采取策略$\pi$所得到的return。

首先，我们可以将从$S_t$出发的轨迹的 discount reward $G_t$ 重新表达为：

$$\begin{aligned} G_t &= R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots \\ &= R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + \dots) \\ &= R_{t+1} + \gamma G_{t+1} \end{aligned}$$

其中，$G_{t+1} = R_{t+2} + \gamma R_{t+3} + \dots$。

这个方程建立了 $G_t$ 与 $G_{t+1}$ 之间的关系。因此，状态值函数可以写成：

$$\begin{aligned} v_{\pi}(s) &= \mathbb{E}[G_t | S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma G_{t+1} | S_t = s] \\ &= \mathbb{E}[R_{t+1} | S_t = s] + \gamma \mathbb{E}[G_{t+1} | S_t = s] \end{aligned}$$

即 Bellman 方程：

$$v_{\pi}(s) = \mathbb{E}[R_{t+1} | S_t = s] + \gamma \mathbb{E}[G_{t+1} | S_t = s].$$

---

接下来进行推导。

第一项 $\mathbb{E}[R_{t+1} | S_t = s]$ 表示对立即奖励的期望值。根据全期望公式（见附录 A），可以计算如下：

$$\begin{aligned} \mathbb{E}[R_{t+1} | S_t = s] &= \sum_{a \in \mathcal{A}} \pi(a | s) \mathbb{E}[R_{t+1} | S_t = s, A_t = a] \\ &= \sum_{a \in \mathcal{A}} \pi(a | s) \sum_{r \in \mathcal{R}} p(r | s, a) r. \end{aligned}$$

该公式给出了在策略 $\pi$ 下，状态 $s$ 处采取动作 $a$ 时的期望奖励。其中$p(\cdot)$是概率，表示了系统模型。

第二项 $\mathbb{E}[G_{t+1} | S_t = s]$ 表示对未来奖励的期望。它可以计算如下：

$$\begin{aligned} \mathbb{E}[G_{t+1} | S_t = s] &= \mathbb{E}_{s'}[\space \mathbb{E}_s[G_{t+1} | S_t = s, S_{t+1}=s'] \space]\\ &= \sum_{s' \in \mathcal{S}} \mathbb{E}[G_{t+1} | S_t = s, S_{t+1} = s'] p(s' | s) \\ &= \sum_{s' \in \mathcal{S}} \mathbb{E}[G_{t+1} | S_{t+1} = s'] p(s' | s) \quad \text{(due to the Markov property)} \\ &= \sum_{s' \in \mathcal{S}} v_{\pi}(s') p(s' | s) \\ &= \sum_{s' \in \mathcal{S}} v_{\pi}(s') \sum_{a \in \mathcal{A}} p(s' | s, a) \pi(a | s). \end{aligned}$$

第一步是如何想到：我们要转换为带有$s’$的，那么就加一个$s’$的条件，加条件之后还要抹去条件，于是再求一次期望（不带下标的$\mathbb{E}$默认是对$s$求期望）。

第二步利用了 $\mathbb{E}[G_{t+1} | S_t = s, S_{t+1} = s'] = \mathbb{E}[G_{t+1} | S_{t+1} = s']$ 这一事实，该事实源于马尔可夫性质，即未来奖励仅依赖于当前状态，而不依赖于过去的状态。

将以上两式代入(3)即可得

$$\begin{aligned} v_{\pi}(s) &= \mathbb{E}[R_{t+1} | S_t = s] + \gamma \mathbb{E}[G_{t+1} | S_t = s] \\ &= \sum_{a \in \mathcal{A}} \pi(a | s) \sum_{r \in \mathcal{R}} p(r | s, a) r + \gamma \sum_{a \in \mathcal{A}} \pi(a | s) \sum_{s' \in \mathcal{S}} p(s' | s, a) v_{\pi}(s') \\ &= \sum_{a \in \mathcal{A}} \pi(a | s) \left[ \sum_{r \in \mathcal{R}} p(r | s, a) r + \gamma \sum_{s' \in \mathcal{S}} p(s' | s, a) v_{\pi}(s') \right], \quad \forall s \in \mathcal{S}. \end{aligned}$$

该方程即 Bellman 方程，它刻画了状态值之间的关系，是设计和分析强化学习算法的基本工具。

下面求解方程。先把Bellman最优方程写成如下形式，

$$v_{\pi}(s)=r_{\pi}(s)+\gamma \sum_{s'\in \mathcal{S}} p_{\pi}(s'|s)v(s')$$

闭式求解

$I-\gamma P_{\pi}$的几个性质

• 可逆
• $(I-\gamma P_{\pi})^{-1} \geq I$

迭代求解

正确性证明

Action Value

$(s,a)$点的Action value定义为：

$$q_{\pi}(s, a) \doteq \mathbb{E}[G_t | S_t = s, A_t = a].$$

可以看出，行动值（Action value）定义为在某个状态下采取行动后可以获得的期望回报。需要注意的是，$q_\pi(s,a)$依赖于状态-行动对$(s,a)$，而不仅仅是行动本身。更严谨地称呼这个值为状态-行动值，但为了简便起见，通常称为Action value。

Action values 和 state values的关系可以由全期望公式得到：

$$\underbrace{\mathbb{E}[G_t | S_t = s]}_{v_{\pi}(s)} = \sum_{a \in \mathcal{A}} \underbrace{\mathbb{E}[G_t | S_t = s, A_t = a]}_{q_{\pi}(s, a)} \pi(a | s).$$

于是有

$$v_{\pi}(s) = \sum_{a \in \mathcal{A}} \pi(a | s) q_{\pi}(s, a).$$

3. 最优状态和Bellman最优方程

我们想求【最优策略】，即$v_{\pi\star}(s) \ge v_\pi(s)$，在所有$s$，对其它所有策略$\pi$。

贝尔曼最优方程：

$$\begin{aligned} v(s) &= \max_{\pi} \sum_{a} \pi(a|s) \left( \sum_{r} p(r|s,a)r + \gamma \sum_{s'} p(s'|s,a)v(s') \right) \\ &= \max_{\pi} \sum_{a} \pi(a|s)q(s,a) \quad s \in \mathcal{S} \end{aligned}$$

矩阵形式（含义是先求最优策略$\pi$，然后解普通Bellman方程求得状态值）：

$$v=\arg\max_\pi (r_\pi + \gamma P_\pi v)$$

求解步骤：

• 先求优化问题：最大q值对应的策略选取概率等于1，其它等于0。可以得到$f(v)=\max_{\pi \in \Pi} (r_\pi + \gamma P_\pi v)$。
• 收缩映射定理：求解$v=f(v)$。

4. 策略迭代和值迭代

目的是求解Bellman最优方程。

Policy Iteration（迭代的是${\pi}_k$）

• Step1：Policy Evaluation，给定$\pi_k$，解Bellman方程得到$v_{\pi_k}$；

$$v_{\pi_k}=r_{\pi_k}+\gamma P_{\pi_k}v_{\pi_k}$$

• Step2：Policy Improvement （要注意只有状态值是${\pi_k}$，其余是$\pi$！）

$$\pi_{k+1} = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi}v_{\pi_k})$$

Value Iteration（迭代的是$v_k$）

• Step1：Policy Update。给定$v_k$，求优化问题得到$\pi_{k+1}$；

$$\pi_{k+1} = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi}v_{k})$$

• Step2：Value Update。求解方程

$$v_{k+1}=r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}}v_k$$

比较：从相同起点开始（将值迭代的初始值设为策略迭代第一次解出的$v_{\pi_0}$），其实仅有第四步之差。

	Policy iteration algorithm	Value iteration algorithm	Comments
1) Policy:	$\pi_0$	N/A
2) Value:	$v_{\pi_0} = r_{\pi_0} + \gamma P_{\pi_0} v_{\pi_0}$	$v_0 \doteq v_{\pi_0}$
3) Policy:	$\pi_1 = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi} v_{\pi_0})$	$\pi_1 = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi} v_0)$	The two policies are the same
4) Value:	$v_{\pi_1} = r_{\pi_1} + \gamma P_{\pi_1} v_{\pi_1}$	$v_1 = r_{\pi_1} + \gamma P_{\pi_1} v_0$	$v_{\pi_1} \geq v_1$ since $v_{\pi_1} \geq v_{\pi_0}$
5) Policy:	$\pi_2 = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi} v_{\pi_1})$	$\pi_2' = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi} v_1)$
$\vdots$	$\vdots$	$\vdots$	$\vdots$

第四步如下图所示，本质都是迭代法求解贝尔曼最优方程，统称为Truncated Policy Iteration。值迭代只迭代了1次，策略迭代（理论上）迭代了$\infin$次，而实际中只能迭代有限次（截断值迭代）。

$$\begin{aligned} v_{\pi_1}^{(0)} &= v_0 \\ \textbf{value iteration} \leftarrow v_1 \leftarrow v_{\pi_1}^{(1)} &= r_{\pi_1} + \gamma P_{\pi_1} v_{\pi_1}^{(0)} \\ v_{\pi_1}^{(2)} &= r_{\pi_1} + \gamma P_{\pi_1} v_{\pi_1}^{(1)} \\ &\vdots \\ \textbf{truncated policy iteration} \leftarrow \bar{v}_1 \leftarrow v_{\pi_1}^{(j)} &= r_{\pi_1} + \gamma P_{\pi_1} v_{\pi_1}^{(j-1)} \\ &\vdots \\ \textbf{policy iteration} \leftarrow v_{\pi_1} \leftarrow v_{\pi_1}^{(\infty)} &= r_{\pi_1} + \gamma P_{\pi_1} v_{\pi_1}^{(\infty)} \end{aligned}$$

5. 蒙特卡洛方法

Policy Iteration中，每次由策略得到$r, P_\pi$时，我们需要系统模型，而MC方法是一种model-free的方法。

均值估计

大数定律估计期望。

MC Basic

从Action value $q_\pi(s,a)$原本的定义出发， 利用期望求。即与环境交互n个episode后，求得其所得奖励的平均值，利用大数定律得到$q_\pi(s,a)$的（无偏）估计。

$$\begin{aligned} q_\pi(s,a) &= \mathbb E[G_t|S_t=s,A_t=a] \\ &= \mathbb E[R_{t+1} + \gamma R_{t+2} + \gamma^2R_{t+3} + \cdots|S_t=s,A_t=a]\\ &≈\frac{1}{n}\sum_i^n g_{\pi_k}^{(i)} (s,a) \end{aligned}$$

注意，MC只是一种Policy Evaluation的方法，我们还需要结合Policy Improvement选出最优策略才能形成完整的RL流程，完整算法流程如下图。

例子表明，随着episode长度的增加，出现了一个有趣的空间模式：**离目标较近的状态比离目标较远的状态更早地具有非零值。**因为从一个状态开始，智能体至少要经过一定的步数才能到达目标状态，然后得到积极的奖励。如果一个片段的长度小于期望的最小步数，则可以确定回报为零，估计的状态值也为零。不过，虽然每个episode必须足够长，但无需无限长。

上述分析涉及到一个重要的奖励设计问题：稀疏奖励，它是指除非到达目标，否则无法获得积极奖励的场景。稀疏的奖励设置需要较长的片段才能到达目标。当状态空间较大时，这一要求很难满足。因此，稀疏奖励问题降低了学习效率**。解决这个问题的一个简单的技术是设计非稀疏的奖励**。例如，在上述网格世界的例子中，我们可以重新设计奖励设置，使得智能体在到达目标附近的状态时可以获得较小的正奖励。通过这种方式，可以在目标周围形成一个"吸引场"，使智能体更容易找到目标。更多解决方法见参考文献（原书英文版P86）。

MC的几个特性：

• offline的

MC Exploring Starts

MC浪费了很多visit的pair（指$(s,a)$对），因为看算法流程，它只更新每个episode起始处$(s,a)$的动作值，而其实每个episode又包含了很多子episode，可以重复利用。

$$\begin{aligned} s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_4} s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_3} s_5 \xrightarrow{a_1} \dots & \text{[original episode]} \\ s_2 \xrightarrow{a_4} s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_3} s_5 \xrightarrow{a_1} \dots & \text{[subepisode starting from } (s_2, a_4)] \\ s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_3} s_5 \xrightarrow{a_1} \dots & \text{[subepisode starting from } (s_1, a_2)] \\ s_2 \xrightarrow{a_3} s_5 \xrightarrow{a_1} \dots & \text{[subepisode starting from } (s_2, a_3)] \\ s_5 \xrightarrow{a_1} \dots & \text{[subepisode starting from } (s_5, a_1)] \end{aligned}$$

此外，一个状态-动作对可能在一个episode中被多次访问。MC Exploring Starts中可以使用两种不同方式更新$q$，如果我们只统计首次访问，这被称为first-visit策略。如果我们统计一个状态-动作对的每一次访问，这样的策略被称为every-visit。

算法流程：

MC Basic的缺点是代理必须等到收集完所有episode后才能更新估计值。而MC Exploring Starts可以克服这个缺点：使用单个 episode 的返回来近似相应的 action 值。这样，当我们收到一个回合时，我们可以立即获得一个粗略的估计。然后可以逐回合改进该策略。

此外，注意Policy Evaluation部分，是用$(s,a)$的所有奖励的平均值来更新$q$，还是根据大数定律，要足够多的访问才能准确。如果某个动作没有得到很好的探索，其动作值可能会被错误地估计，并且即使它确实是最好的动作，策略也可能不会选择该动作。**MC Basic 和 MC Exploring Starts 都需要此条件。**但是在许多场景中很难满足此条件，尤其是那些涉及与环境物理交互的应用。我们可以不需要此要求吗？答案是肯定的，如下一节所示。

MC Greedy

**如果策略在任何状态下采取任何行动的可能性为正，则该策略为软策略（soft policy）。**考虑一个极端的情况，我们只有一个episode。使用软策略，足够长的单个episode可以多次访问每个状态-动作对。因此，我们不需要从不同的 state-action 对开始生成大量 episodes，然后就可以取消 exploring starts 要求。

一种常见的软策略是 ϵ-greedy 策略。它是一种随机策略（stochastic policy），更倾向于选择贪心动作（greedy action），但仍以相同的非零概率选择其他任意动作。

其中，贪心动作指的是**具有最高动作价值（action value）**的动作。具体来说，假设$\epsilon \in [0,1]$，则相应的 ϵ-greedy 策略 具有以下形式：

$$\begin{cases} 1 - \frac{\epsilon}{|\mathcal{A}(s)|} (|\mathcal{A}(s)| - 1), & \text{for the greedy action,} \\ \frac{\epsilon}{|\mathcal{A}(s)|}, & \text{for the other } |\mathcal{A}(s)| - 1 \text{ actions,} \end{cases}$$

$|\mathcal{A}(s)|$ 表示状态$s$可选的动作数。

总结

本章介绍的算法是本书中最早引入的无模型强化学习算法。我们首先通过研究一个重要的均值估计问题引入了蒙特卡洛（MC）估计的概念。随后，介绍了三种基于MC的算法：

1. MC Basic

这是最简单的基于MC的强化学习算法。该算法通过用无模型的MC估计替换策略迭代算法中的基于模型的策略评估步骤来实现。只要样本数量足够，该算法可以收敛到最优策略和最优状态值。

2. MC Exploring Starts

该算法是MC Basic的一种变体。它通过在MC Basic算法的基础上，使用首次访问（first-visit）或每次访问（every-visit）策略来更高效地利用样本。

3. MC ϵ-Greedy

该算法是MC Exploring Starts的一种变体。具体来说，在策略改进（policy improvement）步骤中，它搜索最佳的ϵ-贪心策略，而不是完全贪心策略。这样可以增强策略的探索能力（exploration ability），从而去除**探索起点（exploring starts）**的限制。

6. Stochasitic Approximation

本章没有介绍新的强化学习算法，而是介绍了随机近似的初步方法，例如 RM 和 SGD（随机梯度下降） 算法。与许多其他寻根算法相比，**RM 算法不需要目标函数或其导数的表达式。而 SGD 算法是一种特殊的 RM 算法。**此外，本章中经常讨论的一个重要问题是均值估计。均值估计算法 （6.4） 是我们在本书中介绍的第一个随机迭代算法。我们展示了它是一种特殊的 SGD 算法。我们将在第 7 章中看到 TD 算法具有类似的表达式。最后，“随机近似”这个名称最早由Robbins和Monro在1951年使用。有关随机近似的更多信息，请参见原书参考文献[24]。

RM 算法

用于求解$g(w)=0$方程，使用迭代法：

$$w_{k+1}=w_k-\alpha_k \tilde g(w_k,\eta_k)$$

其中，$\tilde g(w_k,\eta_k)=g(w_k)+\eta_k$，是对$g(w_k)$的一次观测。

优势在于无需函数表达式。

收敛性分析。

【回顾数理方程？】

SGD 算法

SGD是一种特殊的RM算法。

三种随机梯度算法，其实就是所用数据量的多少，类似前面值迭代、策略迭代和截断策略迭代。

$$\begin{aligned} w_{k+1} &= w_k - \alpha_k \frac{1}{n} \sum_{i=1}^{n} \nabla_w f(w_k, x_i), \quad \text{(BGD)} \\ w_{k+1} &= w_k - \alpha_k \frac{1}{m} \sum_{j \in \mathcal{I}_k} \nabla_w f(w_k, x_j), \quad \text{(MBGD)} \\ w_{k+1} &= w_k - \alpha_k \nabla_w f(w_k, x_k). \quad \text{(SGD)} \end{aligned}$$

收敛性分析。性质：在远处时随机性小，表现类似普通梯度下降，离解近时表现随机性大。

7. TD算法

TD算法都属于SGD算法，只是估计的目标函数不一样；都是在求解Bellman方程（或最优方程）。

TD of State value

目标是State value。

$$\begin{aligned} v_{t+1}(s_t) &= v_t(s_t) - \alpha_t(s_t)\left[v_t(s_t) - \left(r_{t+1} + \gamma v_t(s_{t+1})\right)\right], \\ v_{t+1}(s) &= v_t(s), \quad \text{for all } s \neq s_t, \end{aligned}$$

由此形式可以得出，我们的目标是$\tilde g(v_t(s_t))=v_t(s_t) - \left[r_{t+1} + \gamma v_t(s_{t+1})\right]=0$，我们把$g(v)$称之为TD target。

一些重要的 TD 算法性质如下所述。

首先，我们更仔细地研究 TD 算法的表达式。特别地，TD算法可以描述为：

$$\underbrace{v_{t+1}(s_t)}_{\text{new estimate}} = \underbrace{v_t(s_t)}_{\text{current estimate}} - \alpha_t(s_t) [ \overbrace{v_t(s_t) - \underbrace{\left( r_{t+1} + \gamma v_t(s_{t+1}) \right)}}_{\text{TD Target}}^{\text{TD error } \delta_t} ],$$

其中

$$\bar{v}_t \doteq r_{t+1} + \gamma v_t(s_{t+1})$$

称为 TD Target，而

$$\delta_t \doteq v(s_t) - \bar{v}_t = v_t(s_t) - (r_{t+1} + \gamma v_t(s_{t+1}))$$

称为 TD error。可以看出，新估计 $v_{t+1}(s_t)$ 是当前估计 $v_t(s_t)$ 和 TD 误差 $\delta_t$ 的组合。当TD error等于0时，也就是估计趋近于TD Target时。

在更抽象的层面上，TD 误差可以解释为innovation，它表示从经验样本$(s_t,r_{t+1},s_{t+1})$获得的新信息。TD 学习的基本思想是根据新获得的信息纠正我们当前对状态值的估计。innovation是许多估计问题的基础，例如卡尔曼滤波。

此外，其次，上文的TD 算法只能估计给定策略的状态值。 要找到最优策略，我们仍然需要进一步计算 action 值，然后进行Policy Improvement。

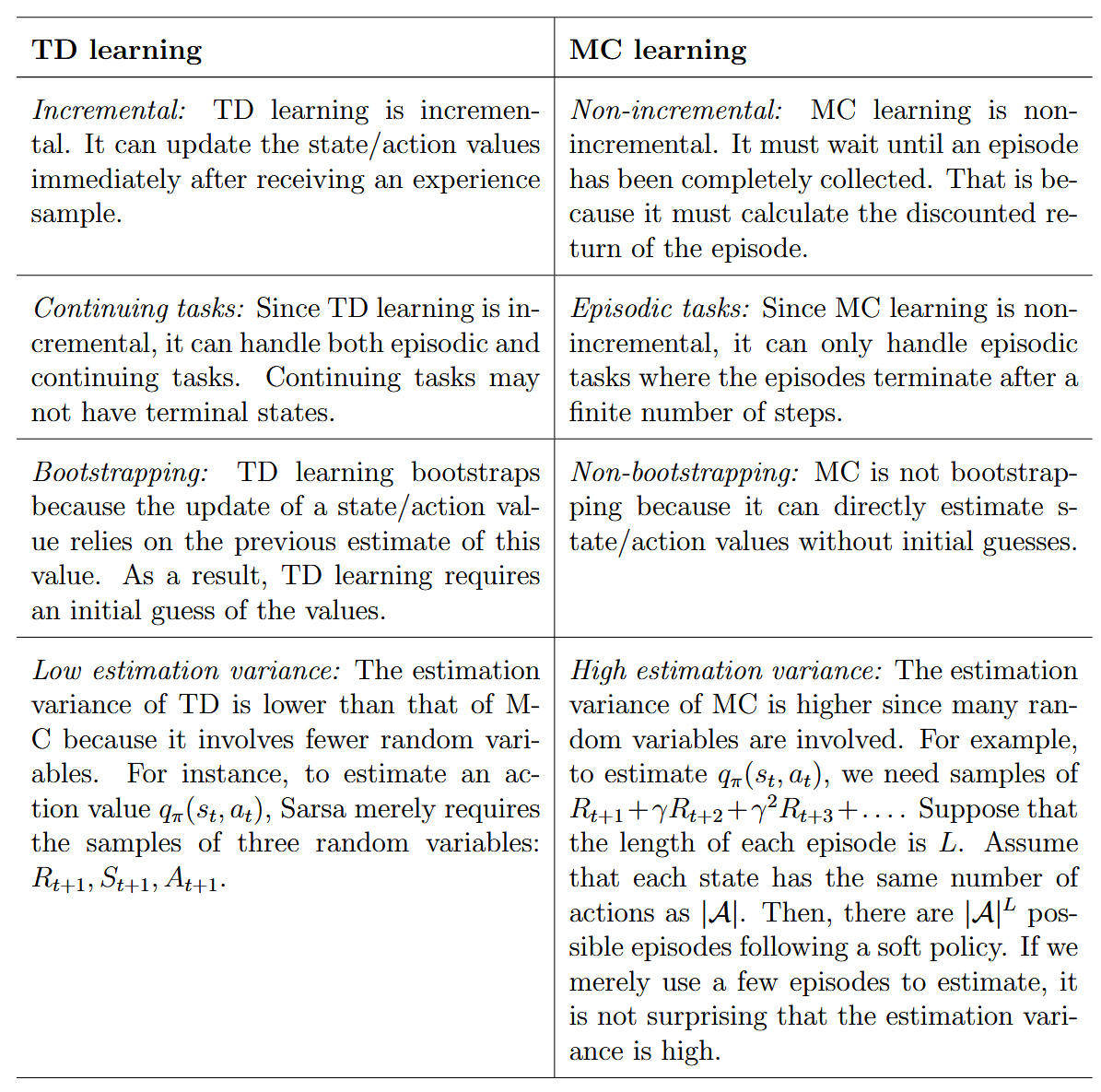
TD和MC区别总结，注意最后一点，variance部分，可以后面推导一下。

TD算法收敛性保证（对学习率的要求）

• Theorem 7.1 (Convergence of TD learning). Given a policy $\pi$, by the TD algorithm in (7.1), $v_t(s)$ converges almost surely to $v_\pi(s)$ as $t \to \infty$ for all $s \in \mathbb{S}$ if $\sum_t \alpha_t(s) = \infty$ and $\sum_t \alpha_t^2(s) < \infty$ for all $s \in \mathbb{S}$.
• 关于学习率 $\alpha_t$，有以下几点说明。
• 首先，条件 $\sum_t \alpha_t(s) = \infty$ 和 $\sum_t \alpha_t^2(s) < \infty$ 必须对所有 $s \in \mathbb{S}$ 成立。注意，在时间 $t$，如果 $s$ 被访问，则 $\alpha_t(s) > 0$，否则 $\alpha_t(s) = 0$。而条件 $\sum_t \alpha_t(s) = \infty$ 要求状态 $s$ 被访问无穷（或足够多）次。这需要满足探索性起点（exploring starts）或使用探索性策略（exploratory policy），以确保每个状态-动作对都可能被访问足够多次。
• 其次，学习率 $\alpha_t$ 在实践中通常选择为一个较小的正常数。在这种情况下，条件 $\sum_t \alpha_t^2(s) < \infty$ 不再成立。不过当 $\alpha$ 为常数时，仍然可以证明该算法在期望意义下收敛 [24, Section 1.5]。

TD of Action value

Sarsa

• 顾名思义，需要$(s_t,a_t,r_{t+1},s_{t+1},a_{t+1})$数据（“sarsa”）进行一次更新。反过来，也就是说只要行动一步就可以更新一次action value（table），然后更新策略。

• 在数学上是求解动作值表示的Bellman方程（给定策略后，求Bellman方程得到action values）

$$q_\pi(s,a)=\mathbb E(R+\gamma q_\pi(S',A')|s,a), \text{for all }s, a$$

• Sarsa算法收敛性保证是由TD算法收敛性推得（Theorem 7.1）。

n-step Sarsa

• 又是一个类似的总结，展开1~n步的关系。注意左侧所有$G_t^{(k)}$都相等，只不过是不同的展开方式。

$$\begin{aligned} \text{Sarsa} \leftarrow G_t^{(1)} &= R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}), \\ G_t^{(2)} &= R_{t+1} + \gamma R_{t+2} + \gamma^2 q_\pi(S_{t+2}, A_{t+2}), \\ & \vdots \\ \text{n-step Sarsa} \leftarrow G_t^{(n)} &= R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^n q_\pi(S_{t+n}, A_{t+n}), \\ & \vdots \\ \text{MC} \leftarrow G_t^{(\infty)} &= R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 R_{t+4} \cdots \end{aligned}$$

TD of Optimal Action value

Q-Learning

大名鼎鼎的Q-Learning，实际上就是TD Target是最优Action Value，而非Action Value。

与Sarsa相比，数学上所求解的方程唯一区别就是增加了max：（求解的不是给定策略的贝尔曼方程，而是贝尔曼最优方程）

$$q(s,a)=\mathbb E(R+\gamma \max_a q(S_{t+1},a)|S=s,A=a), \text{for all }s, a$$

Q Learning既可以on-policy也可以off-policy（或者说，off-policy的算法也可以on-policy实现，前者包括后者），下面给出Q学习 off-policy版本实现（注意更新公式，更新公式是实现算法过程中要用的公式，而数学上求解的贝尔曼方程是数学原理。）

总结

关于on-policy和off-policy。on-policy是收集数据和训练用的是一个策略，off-policy是收集数据和训练可用不同策略。比如MC，Sarsa就是on-policy，而Q Learning是off-policy。

• 根本原因是 Q-learning 是一种求解 Bellman 最优方程的算法，而 Sarsa 用于求解给定策略的 Bellman 方程。求解 Bellman 方程智能评估给定策略，而求解 Bellman 最优方程可以直接生成最优动作值和最优策略。

区别（来自蘑菇书）

• Sarsa算法就是一个典型的同策略算法，它只用一个 π，为了兼顾探索和开发，在训练的时候会显得有点儿“胆小怕事”。它在解决悬崖寻路问题的时候，会尽可能地远离悬崖边，确保哪怕自己不小心向未知区域探索了一些，也还是处在安全区域内，不至于掉入悬崖中。
• Q学习算法是一个比较典型的异策略算法，它有目标策略（target policy），用 π 来表示。此外还有行为策略（behavior policy），用 μ来表示。它分离了目标策略与行为策略，使得其可以大胆地用行为策略探索得到的经验轨迹来优化目标策略。这样智能体就更有可能探索到最优的策略。
• 比较Q学习算法和Sarsa算法的更新公式可以发现，Sarsa算法并没有选取最大值的操作。因此，Q学习算法是非常激进的，其希望每一步都获得最大的奖励；Sarsa算法则相对来说偏保守，会选择一条相对安全的迭代路线。

知乎张斯俊：

• 现在我们来总结一下整个思路： 1. Qlearning和SARSA都是基于TD(0)的。不过在之前的介绍中，我们用TD(0)估算状态的V值。而Qlearning和SARSA估算的是动作的Q值。 2. Qlearning和SARSA的核心原理，是用下一个状态St+1的V值，估算Q值。 3. 既要估算Q值，又要估算V值会显得比较麻烦。所以我们用下一状态下的某一个动作的Q值，来代表St+1的V值。 4. Qlearning和SARSA唯一的不同，就是用什么动作的Q值替代St+1的V值。 - SARSA 选择的是在St同一个策略产生的动作。 - Qlearning 选择的是能够产生最大的Q值的动作。
• 我觉得上面说的有问题，SARSA，QLearning的数学依据是求解Bellman方程，并非他所说的“代替”

8. 值函数

Tabluar -> Function based

值函数近似

IMP

一般对$w$都是线性的，要选取合适的基函数。

Sarsa/QL + function approximation

DQN

经验回放区作用

• 保证均匀分布 => 因为DQN中，我们在求解期望，其中假设了$(s, a)$是均匀分布的（在没有先验的情况下），而收集数据的策略可能是任意的，不一定是均匀分布，所以要从Replay Buffer均匀采样
• 提升采样利用率（同一个$(s, a)$可以用多次）

DQN原理

把QLearning中的Q表格替换成NN。

Double DQN

射击移动靶->射击固定靶

DQN有一个显著的问题：Q值估计偏大，是因为每次都取max。解决的办法：双Q网络。实际上，DQN本身实现的时候就是2个Q网络——一个Target Network，一个不断更新的Network。（每隔一定步数同步他俩）

因此将DDQN技巧应用于DQN，只需要改一行代码。即：

$$r_t+\max_a Q(s_{t+1}, a) \rightarrow r_t+Q'(s_{t+1},\arg\max_a Q(s_{t+1},a))$$

现在我们用每次会更新的Q网络当做$Q$，而Target Network当做$Q'$。

数学原理，为什么可以？（直观理解是$Q$高估的只要$Q'$不选中，反之亦然即可）

9. 策略梯度方法

Metric1：Average Value

1. 选取$d(s)$与$\pi$无关，比如均匀分布；
2. $d(s)$与$\pi$无关，是状态转移矩阵的左特征向量（稳态分布）。

Metric2： Average Reward

Metric的梯度

算法

注意，策略梯度只是一种更新策略的方法，因此还要结合Value Update（或者说，我们还是需要求$q_\pi$），方法有MC和TD。

Policy+MC=REINFORCE算法

蘑菇书笔记（来自李宏毅RL课程）

使用了轨迹形式的表示，但实际和上面的Metric2是等价的。

$$\nabla_{\theta}J(\theta) = \mathbb{E}_\tau [R(\tau)\nabla_{\theta}\log p_{\theta}(\tau)]$$

而赵世钰书中Metric2使用的是状态-动作形式：

$$\nabla_{\theta}J(\theta) = \mathbb{E}_{s\sim\eta, a\sim\pi_{\theta}}[\nabla_{\theta}\log \pi_{\theta}(a|s) \cdot q_{\pi}(s, a)]$$

详细推导过程：（注意其中用到了$\nabla f(x)=f(x)\nabla \log f(x)$，并且期望无法计算，转换为采样）

$$\begin{aligned} \nabla \bar{R}_\theta &= \sum_\tau R(\tau) \nabla p_\theta(\tau) \\ &= \sum_\tau R(\tau) p_\theta(\tau) \frac{\nabla p_\theta(\tau)}{p_\theta(\tau)} \\ &= \sum_\tau R(\tau) p_\theta(\tau) \nabla \log p_\theta(\tau) \\ &= \mathbb{E}_{\tau \sim p_\theta(\tau)} \left[ R(\tau) \nabla \log p_\theta(\tau) \right] \\ &\approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^n) \nabla \log p_\theta(\tau^n) \\ &= \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} R(\tau^n) \nabla \log p_\theta(a_t^n \mid s_t^n) \end{aligned}$$

10. Actor-Critic方法

将Value Function Approximation引入Policy Gradient方法，就得到了AC方法。

第一个：QAC算法